Greedy는 '탐욕스러운, 욕심 많은' 이란 뜻이다.
탐욕 알고리즘은 선택의 순간마다 당장 눈앞에 보이는 최적의 상황만을 쫒아 최종적인 해답에 도달하는 방법이다.
순간마다 하는 선택은 그 순간에 대해 지역적으로는 최적이지만, 그 선택들을 계속 수집하여 최종적인 해답을 만들었다고 해서, 그것이 최적이라는 보장은 없다.
- 즉, 탐욕 알고리즘을 적용할 수 있는 문제들은 그 순간에 최적값들을 계속 수집하여 최종적인 답을 만들어도 최적인 문제들이다.
탐욕 알고리즘 문제를 해결하는 방법
- 선택 절차(Selection Procedure): 현재 상태에서의 최적의 해답을 선택한다.
- 적절성 검사(Feasibility Check): 선택된 해가 문제의 조건을 만족하는지 검사한다.
- 해답 검사(Solution Check): 원래의 문제가 해결되었는지 검사하고, 해결되지 않았다면 선택 절차로 돌아가 위의 과정을 반복한다.
그림으로 한번 보자
여기서 가장 좋은 것(최선의 선택) 이란?

가장 좋은 결과는 root -> 18 -> 100을 거치는 Path가 가장 큰 수를 도출할 수 있다는 것을 알 수 있다.
하지만 그리디 알고리즘은 root 에서 '32'와 '18'의 문제점에서 최적값인 32를 선택하기 때문에 root -> 32 -> 18이 최적값이라고 판단한다.
- 그리디 알고리즘을 사용해 푸는 문제가 나왔을 때 이 조건이 만족되는가?를 생각해 충족되면 사용해야 된다는 것이다.
정리해보자
탐욕 알고리즘을 적용하려면 문제가 다음 2가지 조건을 성립하여야 한다.
- 탐욕 알고리즘이 잘 작동하는 문제는 대부분 탐욕스런 선택 조건(greedy choice property)과 최적 부분 구조 조건(optimal substructure)이라는 두 가지 조건이 만족된다.
- 탐욕스런 선택 조건은 앞의 선택이 이후의 선택에 영향을 주지 않는다는 것이며, 최적 부분 구조 조건은 문제에 대한 최적해가 부분문제에 대해서도 역시 최적해라는 것이다.
- 탐욕적 선택 속성(Greedy Choice Property) : 앞의 선택이 이후의 선택에 영향을 주지 않는다.
- 최적 부분 구조(Optimal Substructure) : 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
- 두가지 조건이 성립하지 않는 경우에는 탐욕 알고리즘은 최적해를 구하지 못한다.
- 이러한 경우에도 탐욕 알고리즘은 근사 알고리즘으로 사용이 가능할 수 있으며, 대부분의 경우 계산 속도가 빠르기 때문에 실용적으로 사용할 수 있다.
- 이 경우 역시 어느 정도까지 최적해에 가까운 해를 구할 수 있는지를 보장하려면 엄밀한 증명이 필요하다.
탐욕 알고리즘은 항상 최적의 결과를 도출하는 것은 아니지만, 어느 정도 최적에 근사한 값을 빠르게 도출할 수 있는 장점이 있다. 이 장점으로 인해 탐욕 알고리즘은 근사 알고리즘으로 사용할 수 있다.
- 어떤 특별한 구조가 있는 문제에 대해서는 탐욕 알고리즘이 언제나 최적해를 찾아낼 수 있다.
- 이 구조를 매트로이드라 하며 모든 문제에서 나타나는 것은 아니나, 여러 곳에서 발견되기 때문에 탐욕 알고리즘의 활용도를 높여 준다.
탐욕 알고리즘을 적용해도 언제나 최적해를 구할 수 있는 문제(매트로이드)가 있고, 이러한 문제에 탐욕 알고리즘을 사용해서 빠른 계산 속도로 답을 구할 수 있다. 그래서 실용적으로 사용할 수 있다.
- 추가적으로 그리디 알고리즘에서 고려해야 하는 상황은 값들이 서로 영향을 주면 안된다는 것을 염두해야 된다.
- Root -> 32 이후에 '7'과 '18'의 문제에서 골라야지 다른 값인 '100'과 '24'에서 영향이 있으면 안된다는 것이다.
근사 알고리즘(Approximation Algorithm)이란?
- 근사 알고리즘(approximation algorithm)은 어떤 최적화 문제에 대한 해의 근사값을 구하는 알고리즘을 의미한다.
- 이 알고리즘은 가장 최적화되는 답을 구할 수는 없지만, 비교적 빠른 시간에 계산이 가능하며 어느 정도 보장된 근사해를 계산할 수 있다.
그리디 알고리즘 문제
많은 블로그들을 찾아봐도 항상 설명하는 거스름돈 문제이다.
당신은 음식점의 계산을 도와주는 점원입니다. 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원 동전이 무한개 존재합니다. 손님에게 거슬러 줘야 할 돈이 N원일 때 거슬러주어야 할 동전의 최소 개수를 구하라. 단, 거슬러 줘야 할 돈 N은 항상 10의 배수이다.

이 문제에서 우리가 생각할 수 있는 것은 '가장 큰 단위의 돈부터 생각하자' 이다. 만약 2240원이라는 돈을 거슬러 줘야 한다고 가정하자.
'최소 개수'를 구하는 문제이므로 가장 큰 단위부터 거슬러주고 나머지를 그 다음 단위의 화폐로 거슬러 주는 것 이라는 해결 방법을 떠올릴 수 있다.
class GreedyAlgorithm {
int solution (int money){
int answer = 0;
int[] change = { 500, 100, 50, 10};
int remain = money;
int i = 0;
while (i < change.length){
if (remain >= change[i]){
answer += remain / change[i];
remain %= change[i];
}
else i++;
}
return answer;
}
}
그리디 알고리즘을 사용해 답을 찾게 된다면, 그 답이 정당한지 생각해봐야 한다.
거스름돈 문제는 가지고 있는 동전 중 '큰 단위'의 동전이 항상 '작은 단위'의 배수이므로(500원은 100원 5, 100원은 50원 2, 50원은 10원 * 5) 작은 단위 동전을 조합해 다른 해가 나올 수 없기 때문에 사용할 수 있다.
활동 선택 문제
활동 선택 문제란, 한 강의실에서 여러개의 수업을 하려고 할 때 한번에 가장 많은 수업을 할 수 있는 경우를 고르는 것입니다. (수업 시작 시간, 수업 종료 시간)
ai = 특정 활동
si = 활동의 시작시간
fi = 활동이 끝나는 시간
ai, aj 활동이 각각 존재할 때, 두 활동의 활동시간이 서로 겹치면 안된다.
- 조건으로는 시작 시간과 끝나는 시간이 같은 경우, 그것도 하나의 수업으로 쳐줍니다.예)
- Exam) si = 3 fi = 3, si = 5 fi = 5
- 또 수업이 끝나고 바로 다른 수업을 시작할 수 있습니다. (1 3, 3 5, 5 7)
- Exam) si = 1 fi = 3 -> si = fi = 5

타임테이블
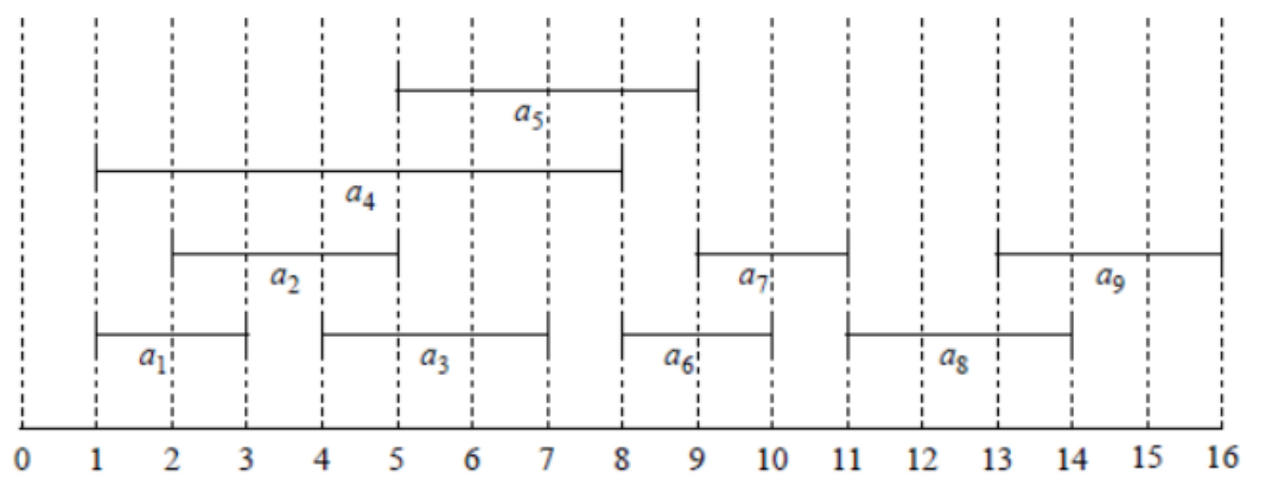
수업들은 하나의 강의실에서 진행해야 하므로 2개의 수업이 중복해서 실행될 수 없다.
- 조합 중 가장 많은 수업을 고르는 것이지, 가장 많은 시간을 할 수 있는 경우를 조합하라는 것이 아니다.
타임테이블을 보면 a1이 가장 빨리 끝나므로 선택합니다. 이 때 a2, a4는 시간이 겹치므로 고를 수 없습니다.
- a2와 a4의 시작 시간(si)가 ai의 종료 시간(fi)보다 작기 때문이다.
최적해를 구하기 위해서는 가장 빨리 끝나는 수업을 골라야 한다.
현재 상태에서 가장 빨리 끝나는 수업이 일찍 끝나게 되면 다음 단계에서 더 많은 활동을 할 수 있기 때문이다.
그리디 알고리즘을 적용해, 빨리 끝나는 강의 순서대로 겹치지 않는 한 강의를 선택하면 다음과 같다.
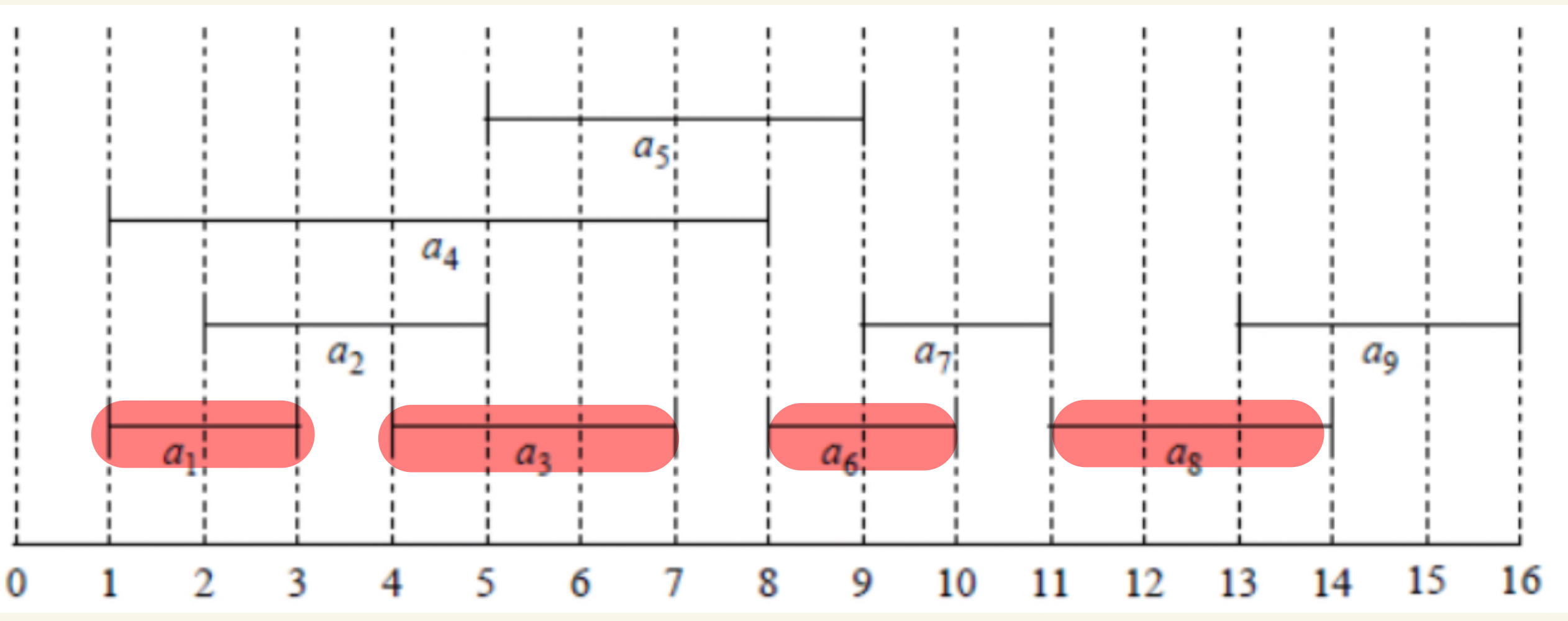
이 문제는 각 상태에서 최적의 선택을 진행했을 때 전체 문제의 최적해에 도달할 수 있는 문제이기 때문에 그리디 알고리즘을 통해 해결할 수 있는 문제가 된다.
'개발 > 코테 & 알고리즘 공부' 카테고리의 다른 글
| 백준 18185번: 라면 사기 (Small) (0) | 2023.03.16 |
|---|
